这是我的阅读笔记喵 (。・ω・。) 因为还没有读完,所以会随时更新噢 ww(少量日文出没,有些实在不知道中文的讲法 QAQ)
点我点我
书名:効果検証入門~正しい比較のための因果推論 / 計量経済学の基礎~
分类:经济学 / 数据分析 / 因果推论
著者:安井翔太
出版社:技术评论社
# selection bias 和 RCT
# 什么是 selection bias
# 效果
假定一个场景:
某便利店为了一个新商品进行了广告宣传,于是这个新商品的销量比以往的新商品销量都要好。
在我们分析之前,首先对一些名词作出解释:
- 效果:
在这个案例里便是销量。 - 介入 / 処置:
在这个案例里面就是广告宣传,若是政策分析的话,也能叫做施策。
回到这个例子,单单是看这句话的描述的话,似乎是因为有了广告宣传,所以这一次的新商品销量比以往都要好。也就是说,广告宣传是原因,而销量变好是结果。但很显然不是这样的,因为我们没有办法排除其他因素的干扰, 比如:
- 服务质量的提升
- 同一时期还有其他的活动
- 发布优惠券
- 与他社的联动
如果忽视了其他因素而单单得出因为有了广告宣传而使得销量提升了这样简单的结论的话,很有可能会导致下一次进行同样的广告宣传但却根本没有达到预期这样的后果,也就是所谓的失算了(专业点来说就是决策失误)。
# 潜在购买量的差
为了说明什么是潜在购买量,我们重新假定一个场景:
某购物网站想要通过发送邮件(邮件内部有优惠券的附件)来增加商品销量。
在这个场景下,假设用户 A 是该购物网站的常客。于是我们能拿到两个数据,一个是用户 A 在邮件发送之前在一定时期之内的购买量,一个便是邮件发布之后在一定时间之内的购买量。 在这个案例里面,第一个数据就是潜在购买量。
在大多数的商业决策中,我们常常依赖这样的数据分析。但是值得警惕的是,单纯这样分析是非常不妥的。
# 错误的决策
在说明问题之前,我们先看看整个事件是如何发生的。
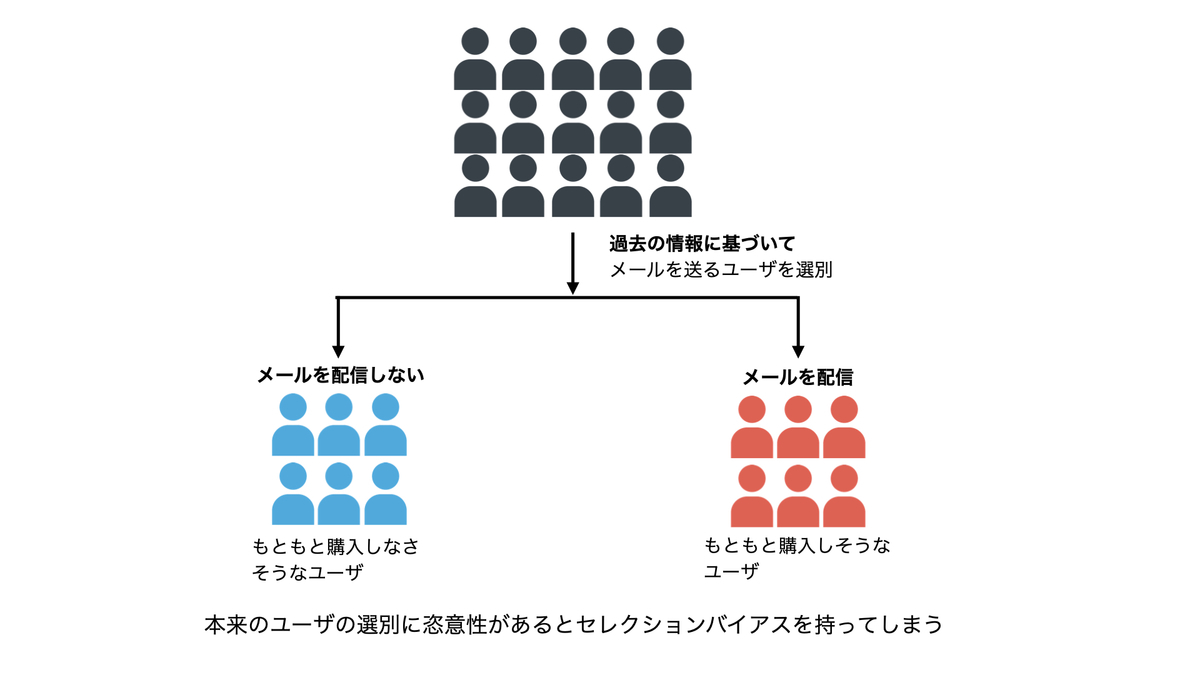
也就是说,网站用户大概是分成两类,一类是原本就要购买商品的用户,另一类则是原本就不买商品的用户。而在一般的商业决策中,商家往往会向前者发送带有优惠券的邮件。更具体来讲,用户被选择发送邮件需要看是否满足以下三个条件:
- 过去的购买量是否到达了一定的数值
- 最近是否有购买
- 买过和优惠券一样的商品吗
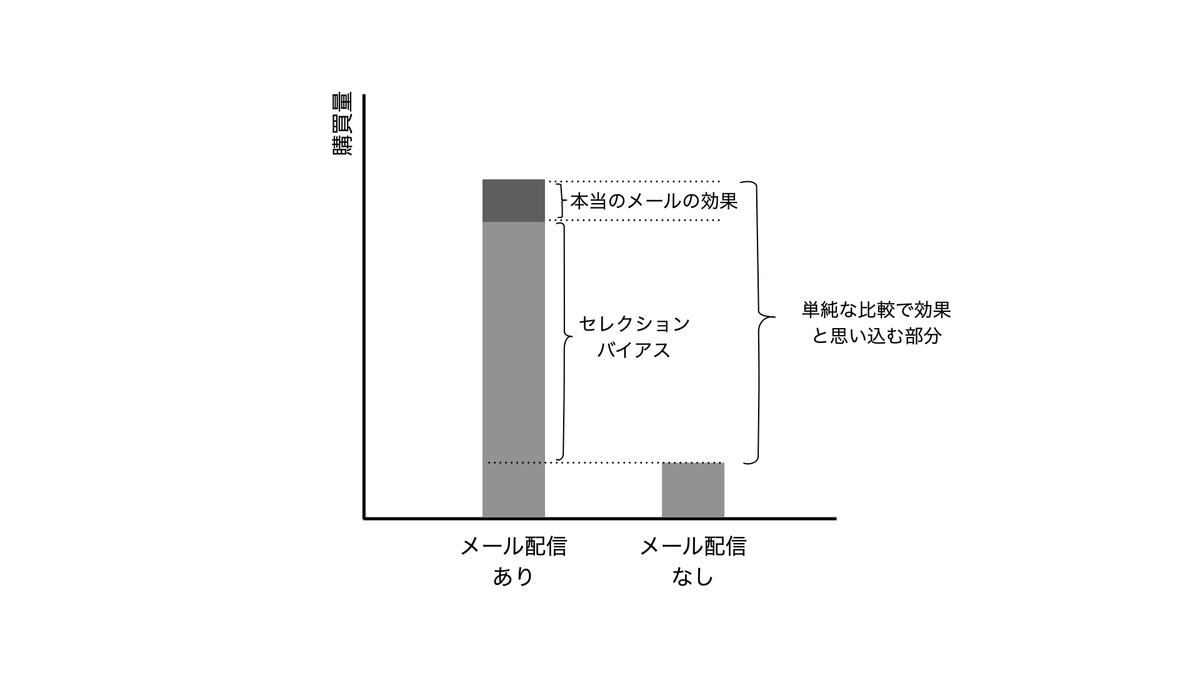
如果满足了其中一样,商家便会选择向他们发送邮件。也就是说,没有被选择发送邮件的用户的潜在购买量原本就比被选择了发送邮件的用户的要少。因此单纯比较发送邮件之后两者购买量之差的话则会存在 selection bias.

像这样,由数据得到的分析结果与实际的效果之间的差便称作 bias,其中由于比较对象之间的潜在不同而产生的 bias 就叫做 selection bias.
# RCT(Randomized Controlled Trail)
到目前为止,想要排除掉其他因素的影响,最好的做法是进行 RCT 实验。
# 真正的「效果」和理想的检验方法
其实最理想的检验方法是,比较两个完全相同的样本。就拿刚刚的例子来说,首先对用户 A 发送邮件拿到用户 A 的购买量之后,再坐时光机器回去在同一个时间节点上不再发送邮件,拿到没有发送邮件的数据。
但是利用目前的科学技术显然是不可能的,因此这就成为了因果推论的根本问题。
因果推论的根本问题是,在比较同一对象在「被介入」与「没有被介入」后的状态是否相同时,因为同个时间点没办法既是「介入」又是「未介入」,所以这个是没办法实现的。
# RCT 检验
既然没办法达到最理想的效果,那么我们只能退而求其次,选择一个相对而言最能信赖的方法,即将介入随机化, 也就是随机选择介入对象。
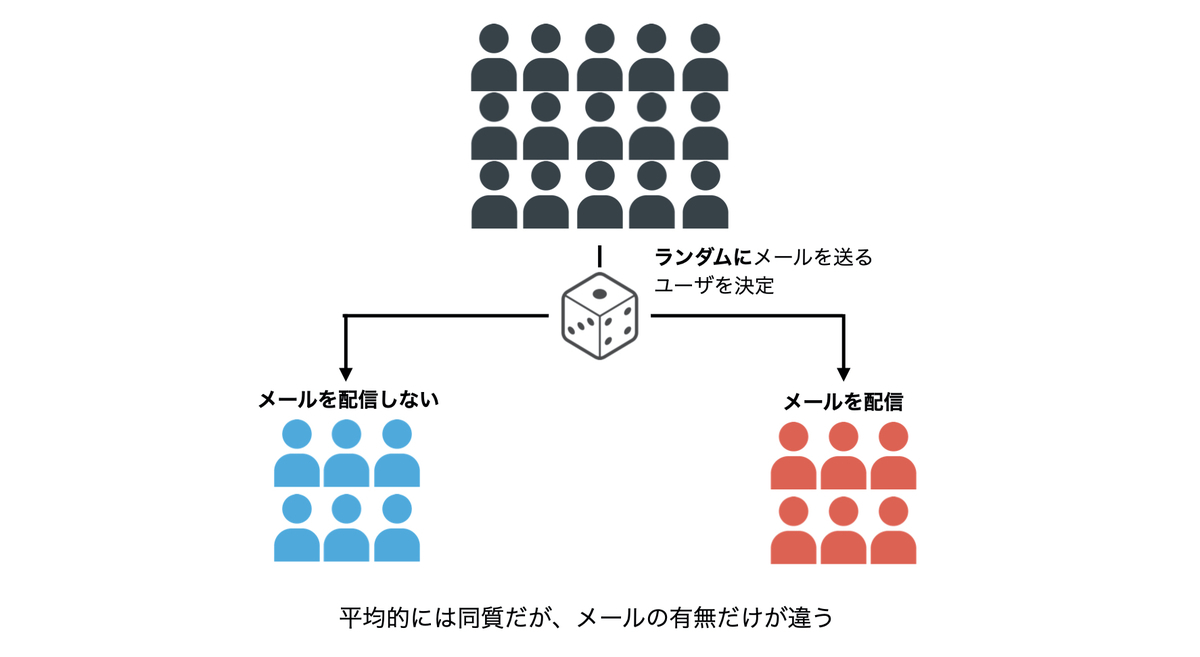
我们可以认为,从平均水平来看,「被介入对象」和「未被介入对象」除了有无配信邮件以外其他方面都是一样的。我们可以通过这样来排除掉其他因素的影响。这样的数据分析的方法便叫作 RCT (Randomized Controlled Trail). 另外,在一些高度数据科学(data science)的公司或机构又将 RCT 叫做 AB test.
# 检验效果的理想方法
到此为止,我们说明了什么是效果和 RCT,接下来我们会使用数学公式对此进行整理。
# 母集団和推定
观测数据的背后潜在的所有能观测到的数据称为母集団(不太清楚中文的讲法)。但是我们没有办法收集到所有的数据,所以只能分析手里头有的数据,这个过程叫做推定。但是值得注意的是,我们想要通过推定来知道母集団的某一个特征,而其他特征作为干扰项是需要被我们排除在外的。
# Potential outcome framwork
我们首先考虑母集团的效果。假定有某个样本(按照上面的例子的话就是用户 A)i,设 为是否配信邮件,其中 为配信邮件, 为不配信邮件,如下:
接下来,我们有假定 为介入(或没有介入)之后的购买量,其中 表示没有邮件配信时的购买量,而 则表示邮件配信之后的购买量。如下:
因此,整体的效果可以通过以下算式来表现:
像这样,我们认为对于每个样本(用户 A)来说,介入和没有被介入的差值(即 和 )便是 potential Outcome Framwork.
# 基于 potential outcome framwork 的介入效果的推定
现在假定一组数据,如下表:
- 第 i 行就是用户 i
- 用户 i 的购买量是 Y
- 指不配信邮件时的购买量, 指配信邮件时的购买量
- 是否配信邮件用 Z 来表示
表 1.1 用户的购买量(拟定数据)
| i | Y | Z | ||
|---|---|---|---|---|
| 1 | 300 | 300 | 400 | 0 |
| 2 | 600 | 500 | 600 | 1 |
| 3 | 600 | 500 | 600 | 1 |
| 4 | 300 | 300 | 400 | 0 |
| 5 | 300 | 300 | 400 | 0 |
| 6 | 600 | 500 | 600 | 1 |
| 7 | 600 | 500 | 600 | 1 |
| 8 | 300 | 300 | 400 | 0 |
| 7 | 600 | 500 | 600 | 1 |
| 10 | 300 | 300 | 400 | 0 |
由前述所说得知,效果便是 与 之间的差值,因此上表的所有用户的效果都为 100,即配信了邮件之后,购买量会比没有配信邮件时多出 100. 因此,介入效果(τ,读作たう)可以通过以下算式来表示:
但是值得我们注意的是,我们能够得观测到的数据只有 Y 和 Z ,因此我们无法算出想要的 τ 值。所以,我们不是着眼于 与 ,而是去比较配信的群体和没有被配信的群体,然后去考虑平均效果。
(未完待续,更新于 2023/8/27)
